ემპირიული ალბათობა წარმოადგენს დაკვირვებას, მოვლენის აღწერას, რომელიც განსხვავებით ფუნდამენტური კანონისაგან არ იძლევა მოვლენის ზედმიწევნით აღწერას, არამედ მხოლოდ საერთო სტატისტიკურ ინფორმაციას გარკვეული სტოჰასტიკური პროცესის მასშტაბით. შესაბამისად ალბათობა არ იძლევა საშუალებას გვქონდეს ზედმიწევნით სრული და უნიკალური აღწერა კონკრეტული პროცესისა (მათ შორის, დროში, შედეგების ზედმიწევნით წინასწარმეტყველებით), მაგრამ გვაძლევს აღწერას, რომელიც არის გარკვეული ინფორმაციის მატარებელი პროცესის თვისებებისა და არა ინდივიდუალური, არამედ განმეორებით ჩატარებული ცდების საერთო მოსალოდნელი შედეგისა, რაც კავშირიც ვლინდება ე.წ. ასიმტოტური ალბათობის თეორიის ფარგლებში (დიდ რიცხვთა კანონები, კონვერგენციის თეორიები).

თეორიული ალბათობის საფუძვლები ჩამოყალიბებულია რუსი მათემატიკოსის, კოლმოგოროვის მიერ, რომელიც ალბათობიას განიხილავ მათემატიკური საზომის კონკრეტულ შემთხვევათ. განიხილება ალბათობის სივრცე: (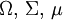), სადაც Σ არის სიგმა-ალგებრა, μ კი ნორმალიზებული ზომა მასზე, რომელიც შესაბამისად ალმაყოფილებს სამ აქსიომას:

-

-

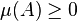
- μ(Ω) = 1

Ωს წევრებს ეწოდებათ ალბათობის პროცესის შედეგები, მათ ნებისმიერი კრებულ კი - ხდომილება.

ალბათბის სივრცე შეიძლება იყოს სასრული და უსასრულო. ალბათობის სივრცეში შეიძლება განიხილო შემთხვევითი ცვლადი, რომელსაც ალბათობის სივრცე (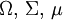) გადაჰყავს სტანდარტულ სივრცეში , სადაც რეალურ რიცხვთა სიმრავლეა, B კი ბორელის სიგმა-ალგებრა მასზე. შესაბამისად ალბათობის ზომა გვაძლევს ალბათობის სიმკვრივისა და კუმულატიური სიმვრივის ფუნქციებს რეალურ რიცხვთა სიმრავლიდან [0,1] ინტერვალისაკენ. ამგვარად ტრანსფორმირებულ ალბათობის სივრცეს აქვს შედეგობრივი მახასიათებლები: მათემატიკური მოლოდინი, დისპერსია და მომენტები, რომლებიც ალბათობის სივრცის გარკვეული ინფორმაციის მატარებელნი არიან.

ალბათობის თეორიის მრავალ შედეგთაგან აღსანიშნავია დიდ რიცხვთა კანონები და კონვერგენციის თეორემები.

პრაქტიკული ალბათობის თეორის მოიცავს პარამეტრულ და არაპარამეტრულ კვლევას და ჰიპოთეზების ტესტებს და მრავალ ემპირიულ მოდელს. წრფივი რეგრესია ამ სფეროს ერთ-ერთი ყველაზე ფართოდ გავრცელებული ინსტრუმენტია